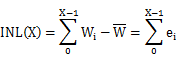最近有涉及到在带通结构的 Sigma-Delta DAC 中应用 DWA （Data Weighted Averaging）算法的工作，看到有些论文解释的不算很明白，这里谈谈自己关于 DWA 动态匹配实现电路元件的 mismatch- shaping 的一些理解。
首先，考虑电路中存在 M 个元件，其元件序号为 0 ~ M-1，第 i 个元件实际值为 Wi，对应的误差值为 ei ，可以定义：
这里可以将其理解为在无 DWA 时，电路中输入数据 X （即选择 X 个元件输出）时所带来的输出误差。
下面考虑对于基本的一阶 DWA 算法的 1-z-1 的 mismatch-shaping 特性的推导，下图所示为 M=7 时的 DWA 算法示例：
对于弱反型（weak inversion）或者说是亚阈值区（Sub-threshold）的 MOS 器件的匹配问题，很容易产生的一个想法就是由于电流和阈值的指数关系，器件的 matching (匹配)会变差。实际上，这种想法并不全然正确，这一问题在 ’Analog-Design-Essential‘ 书中亦有分析，这里简单叙述一下：
首先如下面的基本电流镜电路，考虑阈值 Vth 的 mismatch 由经由 MOS 管的跨导 gm 变为 Iout 的 mismatch，同时 uCox/2（也即K‘）和宽长比的 mismatch 直接影响输出电流，可以容易推出其输出电流 Iout 的 mismatch 为：
ΔIout/Iout=ΔVth*(gm/Id)+ΔK‘/K’+Δ(W/L)/(W/L)
继续阅读
在集成电路的设计中，常需要考虑电路中各元件的匹配（mismatch）问题，特别在 foundry 的 model 没有提供统计参数来做 monte-carlo 分析时，需要设计人员利用 foundry 的文档中的参数对集成电路中器件的随机失配做一些估计，因此有必要了解一些器件匹配的统计模型。这里对这一问题简单来小结一下。
关于集成电路中器件的随机失配，可以用一简单的模型来加以描述：
其中，A 为器件随机失配的参数，通常在设计手册中给出；B 为测试带来的失调，通常可认为为零； W 和 L 为器件的宽长(um单位)； S 为对器件间距的敏感参数； D 为两器件的间距。