最近有被问到相位噪声和时域抖动的关系,虽然在之前关于 jitter 的小结里面有提到过由 phase-noise 积分计算 jitter, 但是这一变换具体由何而来,理解的还不是很清楚,为此回去把随机信号的基础翻了下(主要是参考了 “ The Designer’s Guide to Jitter in Ring Oscillator ” 中关于噪声的部分),也在这里记录一下..
继续阅读
标签归档:Jitter
关于 spur 转换到 jitter 的计算
之前有写过关于 Reference Spur 的总结,里面有提到关于 spur 与 jitter 的转换,这里具体来谈下由 PLL 的 spur 来计算 peak-peak jitter 的问题
对于 VCO 的输出信号,考虑控制线上存在小的交流分量,此时的 VCO 输出可写为:
其中, ωo 为 VCO 的振荡频率, ωm 为 Vctrl 上的交流分量的频率,Δf 为最大频率偏移, θp ( 或 Δf/fm ) 为最大的相位偏移。
继续阅读
关于 jitter 的小结
在这里把看的有关 jitter 的内容整理一下:
Jitter is the undesired deviation from true periodicity of an assumed periodic signal in electronics and telecommunications, often in relation to a reference clock source. — from wikipedia
通信系统中的 Jitter
在文献【1】中提到,‘timing variations’可以分为两类:
- Wander: Timing variations that occur slowly
- Jitter: timing variations that occur more rapidly
两者之间一般以 10 Hz 为分界。
Matlab 由时域仿真结果计算 jitter 的脚本
这里简单谈下由时域仿真结果计算 jitter 的方法。
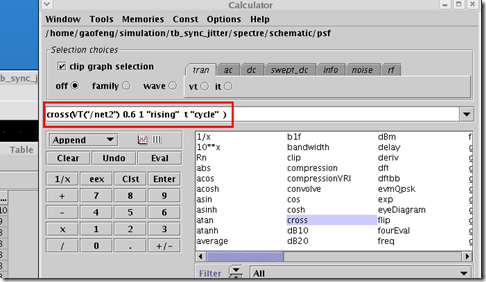
关于如何计算 jitter, 这里的方法主要分为两步,首先在 Cadence 仿真中得到时钟信号过零点时刻的数据,然后利用 matlab 对此数据处理,从而得到 clock jitter 以及时钟周期的直方图(histogram)。
对于过零点时刻的获取,主要可以通过 calculator 中的 cross 函数对 spectre 时域仿真的时钟信号的处理来得到,如下图中所示。
Sampling jitter 的两种考虑方法
最近看 Maloberti 的数据转换器的书,里面在分析对于采样时钟的 sampling jitter 的要求,具体的角度和以前看到的 J.Baker 书中的有些差别。这里,把他们具体的分析都记录下,以方便对比。
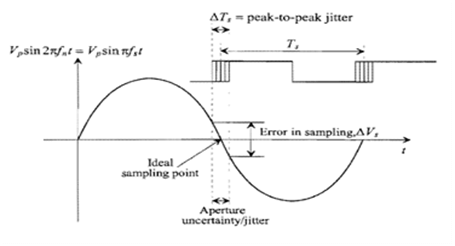
J.Baker 的混合信号书中对于 aperture uncertainty (jitter) 的分析方法, 主要是考虑后面的 ADC的,使得 sampling jitter 引入的误差小于1/2 LSB.
关于抖动时钟的模型
在 IC 设计(如 ADC 电路等)中,有时候要考虑时钟抖动(clock jitter)的影响,通过在设计初期加入带有抖动的时钟模型可以较快的判定其影响。
关于 clock jitter 具体的仿真模型,J.Baker 的混合信号书中提到的方法是利用 spice 中的 SFFM 模型,即单频率频率调制源(Single-Frequency-Frequency-Modulation):
SFFM (Vo Va ...)
也即为如下的函数:
Vsffm(t)=Vo+Va*sin[2*pi*Fc*t+MDI*sin(2*pi*Fs*t)]
在这里,调制率 MDI 决定了峰峰值相位偏移,即 2*MDI=2*pi*dt/Ts=2*pi*dt*Fs, (Ts=1/Fs)
故而,可以简单的认为 peak-peak jitter:dt=MDI/(pi*Fs)
在得到此抖动的正弦信号后,通过理想判决器(比较器)可以将其转换为我们所需的抖动时钟信号
这种方法的问题主要在于:得到的 clock jitter并非随机;J.baker 也在书中也提出通过设置 Fs 与仿真时间来使其更接近实际情况。
事实上,通过 Verilog-A 工具可以更容易的仿真时钟抖动的影响,一个简单的想法是利用 verilog-A 中的 transition 语句在 delay 中引入随机(利用 $rdist_normal 函数),可参考的部分 Verilog-A 代码如下:
继续阅读