最近的工作中接触了一些开关电容电源变换器（电荷泵）的内容，在翻阅一些论文之后，感觉还是Michael. Douglas. Seeman 在他的论文中介绍的分析方法比较清楚，这里把里面的charge-multiplier-vector 方法在 0.5x 电荷泵上做一些分析和简单的验证。
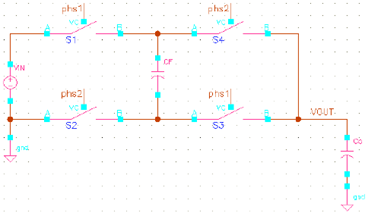
下图所示为基本的 0.5x 电荷泵，在 phase 1：开关S1, S3 闭合，S2和S4 断开, 电容Cf ( flying capacitor ) 和输出电容 Co 串联接到输入电压源; 在 phase 2：开关 S2, S4 闭合，S1 和 S3 断开, Cf 与Co并联到输出.
之前介绍了两个电流模式控制的开关变换器的分析模型中，变换器都是处于连续导通模式，下面介绍一下变换器工作于非连续导通模式时，具体的电流控制模式的分析。
上图所示为基本的buck变换器，类似之前的分析，在DCM工作时，我们可以得到开关网络端口电压的平均值：<v1>=vg， <v2>=vg*d1+v*d3
之前介绍了电流模式控制的开关变换器的一阶简化模型，在简化分析中，我们假设电感电流的均值等于控制电流，在实际中电感电流的ripple并不总是能忽略的，因此需要更为完善的等效模型，这里我们对此做一些小结。
首先，对于实际电感电流的均值（与控制电流的关系），我们可以通过下图加以考虑。
上图所示为斜坡补偿后的电感电流的波形，可以看到实际电感电流的峰值与控制电流的差别为ma*d*Ts . 考虑电感电流的峰值与其平均值相差为其纹波大小，在一般瞬态情况下（包括周期开始结束时电流不等）d时段的ripple为0.5*m1*d*Ts,，d’ 时段的ripple为0.5*m2*d’*Ts, 则电感电流的均值可以写为：
这里接着把电流模式控制的开关变换器的一阶简化模型的分析方法小结一下。
下图所示是包含电流模式控制的开关变换器的系统框图，整个系统控制环路包括内部的电流控制环路和外部的电压反馈环路。
为设计外部电压反馈环路，需要找出ic到输出的传输函数（等效电路）或者ic导致的占空比d的变化以利用之前分析开关变换器等效模型的结果。
这里把关于开关变换器在电流控制模式下的50%占空比问题（亚谐波振荡问题）以及对应的斜坡补偿方法来做些小结。
下图所示为电流模式控制的buck变换器，他同时包含了电流控制和电压控制回路，其中中间框中的部分为电流控制环路。
这里的电流控制环路中，mos开关的电流与控制电流相比较，输入到RS触发器的reset端，从而控制开关的导通时间（占空比）。因此实际上，这一环路将使得开关电流的峰值与控制电流相等，如下图中所示。
