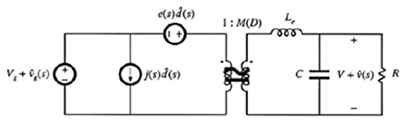
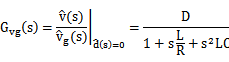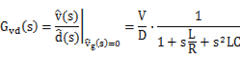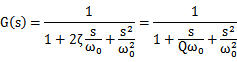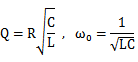在之前的文章中得到了buck结构的等效电路的标准形式，具体如下图中所示:

其中M(D)=D, L_e=L, j(s)=V/R, e(s)=V/D²

通过上面等效电路，我们可以进一步得到buck电路的输入电压到输出电压和控制到输出电压的小信号传输函数。

对于输入电压到输出：

对于控制到输出：

注意在计算控制到输出时，将输入小信号电压源v_g(s)短路, 这也使得j(s)d(s)的小信号电流源不在后续的计算中出现。

考虑到上面的传输函数的分母的形式，可以把后面部分取出写成二阶系统的标准形式：

对应前面的buck结构中的LRC电路：

通过简单的计算，可以看到G(s)在dc和ω₀出对应的幅度为1和Q，在‘Fundamentals of Power Electronics’书中将G(s)的幅频曲线的peaking就认为是dB20(Q)，这实际是一种近似，实际的峰值的计算在Allen那本书的附录中有相应的介绍。

下面我们通过具体的例子来验证一下前面的小信号传输函数，以G_vg(s)为例。

考虑buck变换器的输入V_g为3.3V，输出为1.65V，则占空比D=0.5，负载电阻为1Ω，对应电流为1.65A，开关频率为200KHz，也即周期Ts=5us，选取电感电流的ripple为15%，电容电压的ripple为1%，通过之前具体ripple的计算方法，得到L约为8uH，C约为10uF。

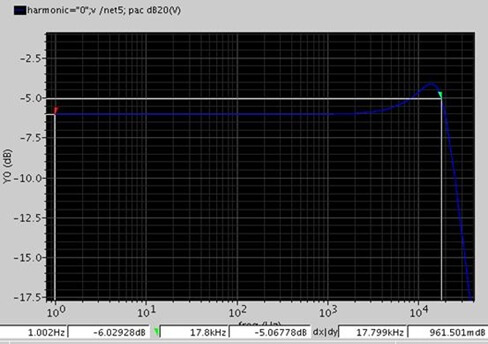
通过计算可以得到，以G_vg(s)的DC gain为-6dB，f₀=17.8KHz，Q=1.118 (对应0.97dB)

在 cadence 中对这一 buck 电路做 pac 分析， 得到的幅频曲线如下， 在频率17.8K 对应幅度约为 -5dB， 可见于计算结果还是很相近的.