最近有涉及到在带通结构的 Sigma-Delta DAC 中应用 DWA (Data Weighted Averaging)算法的工作,看到有些论文解释的不算很明白,这里谈谈自己关于 DWA 动态匹配实现电路元件的 mismatch- shaping 的一些理解。
基本的 DWA 算法的原理
首先,考虑电路中存在 M 个元件,其元件序号为 0 ~ M-1,第 i 个元件实际值为 Wi,对应的误差值为 ei ,可以定义:
这里可以将其理解为在无 DWA 时,电路中输入数据 X (即选择 X 个元件输出)时所带来的输出误差。
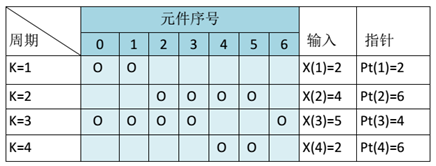
下面考虑对于基本的一阶 DWA 算法的 1-z-1 的 mismatch-shaping 特性的推导,下图所示为 M=7 时的 DWA 算法示例:
这里定义 Pt(k) 为第 k 个周期完成后,下一周期选择元件的起始位置序号
为简化分析,考虑 k 次输入不使其越界(即不考虑 Mod 作用),则第 k 次输出带来的误差为:
将其转换到 Z 域,可以看到
可见,DWA 等效的对电路的输出误差实现了一阶差分,也就所谓的 Mismatch-Shaping。
带通结构中 DWA 算法的实现
对于之前分析的结果,若再利用 N-path filter 的方式 (其中的单路相当于工作于 Fs/N,因此到 z -> zN 的变换),对 DWA 采用 N 个指针以时间交织的方式工作,则可以实现 1-z-N 的特性的 mismatch-shaping,对应的 notch 频率为: 0,Fs/N, 2Fs/N, 3Fs/N, … ,从而可以应用到带通结构的电路中。
进一步考虑 1+z-N 的特性, 可以看到其对应的 notch 频率在于 Fs/2N, 3Fs/2N, 5Fs/2N, … 。对比1-z-N 的特性,可见所需的指针数量减小了一半,因此对于带通特性的输入(如BP-SDM),可以采用1+z-N 方式的 Mismatch-shaping。由于之前提到类似 N-path filter 的处理方式,下面只分析 1+z-1 特性 DWA 的工作原理。
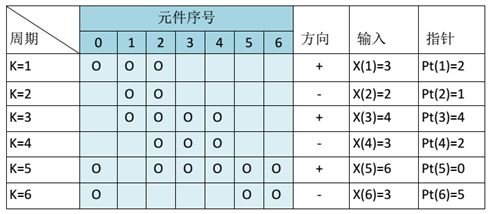
下图是实现 1+z-1 的DWA 算法示例:
当 k 为奇数, Pt(k)=Pt(k-1)+X(k)-1 mod M
当 k 为偶数, Pt(k)=Pt(k-1)-X(k)+1 mod M
为方便分析,考虑 k 为偶数,且指针不发生越界(不考虑 Mod 作用),k 与 k-1 时刻输出的误差:
并且有:
转到 Z 域,可以看到
也即:
同样考虑 k 为奇数可以得到类似的结果,只是此时 INL 考虑以-方向选取的误差,因此残留的疑问主要在于如何统合这两个结果,另外一个问题是当指针发生越界(也就是通过 mod 取余数)时具体如何分析。
当然,通过仿真结果验证这样的 DWA 算法仍然是可行的,下面给出了在 BP-SDM 输出码流加上 DWA 的结果的对比,DWA 实现的为 1+z-4 的 mismatch-shaping。
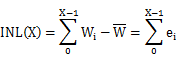
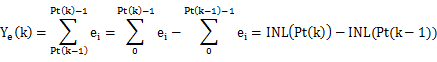
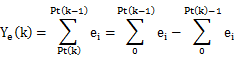
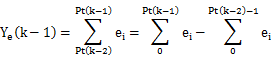
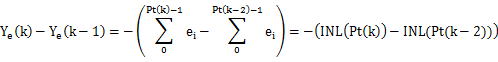
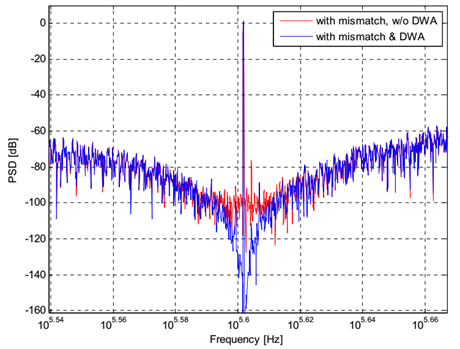
这个推导里面,k时刻的误差指的还是第K次的输入造成的误差,因此其实证明的结果是第K次的误差被整形。而且INL(Pt(k))这个量的含义还是有点奇怪的。实际上要证明整形效果,应该要证明的是第K次及此前K-1次的误差加起来后的总误差被整形才可以吧。
M个器件单独使用时,存在一个最大的误差,INL(Pt(k))小于这个最大误差(每使用整数个M器件,INL(Pt(k))被清零),因此可以理解为最大误差被噪声整形?
“应该要证明的是第K次及此前K-1次的误差加起来后的总误差被整形才可以吧”, 低频就会被噪声整形,“第K次及此前K-1次的误差加起来” 偏向于接近直流的极低频了,只要频率低于采样频率就会被噪声整形,不过就是频率越低整形效果越好?(比如k和k-1的误差之和也没整形,小于单次的误差,不过整形效果没有那么好)
请问一下作者,这篇文章的分析,有没有文献可以方便分享一下?我看UNDERSTANDINGDELTA-SIGMA DATA
CONVERTERS 这本书也只是浅显的说明了一下。看了很多文献都是不得要领,感觉您的分析浅显易懂。
基本上就是看的这本书里的内容加上自己的理解