最近有被问到相位噪声和时域抖动的关系,虽然在之前关于 jitter 的小结里面有提到过由 phase-noise 积分计算 jitter, 但是这一变换具体由何而来,理解的还不是很清楚,为此回去把随机信号的基础翻了下(主要是参考了 “ The Designer’s Guide to Jitter in Ring Oscillator ” 中关于噪声的部分),也在这里记录一下..
首先,关于 Phase-Noise L(f), 一般定义为 Single-sideband noise-to-carrier ratio, 在通过窄带调频的假设后也可推出下面的关系(也有些论文中直接采用下面的定义)
其中 SФ(f) 为瞬时相位波动 ( phase fluctuations ) Ф(t) 的单边带频谱
Ф(t) 实际上可以认为是随机信号,由 Wiener-Khinchin 理论,随机信号的功率谱密度 psd 实际上是其自相关函数的傅里叶变换,故此
而通过傅里叶逆变换,相应的有
*关于相关函数的定义: Rxx(t, t+τ)=E{X(t)X(t+τ)}, 其中 E{x} 为 x 的期望值
对于 phase-jitter,这里可以认为就是瞬时相位波动 Ф(t) 的标准差 ( standard deviation ), 而考虑 Ф(t) 的方差:
在考虑 Ф(t) 期望值为零,且引入自相关函数的表示之后,实际上可以得到
由之前 psd 的傅里叶逆变换的表达式,可以得到
之后,考虑到 SФ(f) 的定义, Phase-Jitter 可以表示为如下:
考虑相位和时间的关系以及 SФ(f) 和 L(f) 的关系,最终可以得到 absolute jitter:
以上就是相噪积分得到 jitter 的来源,剩下的问题主要是对与频谱的单/双边带以及积分限的变化的理解还有些含糊,看有机会在之后的工作中能不能再弄清楚一些。
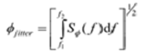
请教一下仁兄,phase noise dbc 转化成幅度后平方积分,得到的单位为啥是弧度? 通常我们把phase noise 第一步得到弧度后除以2pi*f0 得到jitter , 我刚接触这个不太理解,为啥第一步得到的单位是弧度?
想请教下相噪换算抖动的时候积分区间怎么算 比如为什么一般是12kHz~20MHz
您好,我也有这个疑问,积分上下限应该如何选择?请问您现在有理解了吗?谢谢!
这个方向后来没做太多工作
您好!我想向您请教关于jitter的问题。
对相位噪声进行积分,得到的是连续相位变化的rms值。但是实际测量abs jitter时,我们的jitter定义应该是过零点和理想位置的变化值,也就是我们应该获得的过零点偏差值的功率谱密度。
我看了一些论文,也看了designer guide,感觉相位噪声功率谱密度和过零点偏差值的功率谱密度应该不是等效的。
这样,积分出来的相位抖动rms值应该就不是实际测量的jitter。
不知道是我哪里理解错了,麻烦给些指点或者相关的参考论文
谢谢!
过零点偏差,这个乘以频率就是相位偏差吧
哇 我也一直有这个疑惑 实际过零点jitter和根据相位噪声求jitter这两者之间有什么联系吗
相噪的功率谱密度与普通电压电流噪声的功率谱密度有差别么?除了变量是相位以外
从定义的方式看应该是一样的吧
看来是在求自相关时对tao进行了积分,不是对绝对时间的积分
感觉自己对负频率还是理解不够.
请问相位功率谱的f和相位噪声L(f)中的f是频率偏移还是正常的频率?
频偏