最近打算把 PLL 相关的东西清一下,目前主要进展到 Spur 相关的内容,发现具体分析 Reference Spur 的资料都比较少,除了 Dean Banerjee 的书里面在应用层次谈到一些外,基本上就只有李宇根 ( Woogeun Rhee ) 的论文有比较详细的介绍。但是,李宇根在 ISCAS 的论文和他自己的博士论文中关于 Spur 的算式都有差别,因此打算在这里把自己关于这些问题的想法梳理一下.
所谓的 Spur: Any undesirable non-harmonic signal present at the output spectrum
按照 Dean Banerjee 的说法, spur 可分为:
- Reference Spur : Spur的 offset frequency 在 PFD 的参考时钟频率(及其谐波处)
- Non-reference Spur : 其他的 spur, (源自外部环境的干扰或内部的其他问题)
- Fractional Spur : 主要是 Fractional-N PLL 中的 spur
这里主要考虑 Reference Spur 的问题
关于 spur 的基本计算
对 supr 的分析,一般用的是窄带调频的方法,我们考虑 VCO 的控制电压上叠加一个波动 Vm:
由 VCO 的特性,可以得到最大的频率偏移为:
在这里可以定义一个调制因子 ( modulation index ) m :
这样,频率调制的信号可以表示为 m 参量的 Bessel 函数,对于窄带调频, J0(m)=1, J1(m)=m/2, 而 J2(m), J3(m) .. 近似为零。
故,信号的 Spur (也即 sideband-to-carrier ratio ) 可以表示为如下:
我们也可以利用类似于引入 phase-noise 时的分析方法来对加深对 spur 的理解。考虑下面的 spurious 信号:
考虑信号幅度不变,且相位的偏移为正弦变化,则上式可以进一步写为:
注意, 上式可以推出 S(t) 的最大频率偏移为 Δf, 因此之前的调制因子* m=Δf/fm
将 m 代换上式,并考虑三角函数的展开,可以得到
考虑 m<<1, 则上式可近似为:
可见在频偏 fm 处的幅度为 m/2, 与之前提到的 bessel 函数表示的 J1(m) 相同。
*注意, 之前的 S(t) 中实际上调制因子 m 也代表了信号的最大相位偏移,因此可以得到 jitter 和 spur 的量化关系:例如,若已知 peak-peak 的 deterministic jitter 为0.01UI, 则对应的最大相位偏移 m=0.01*0.5*2*Pi, 因此 P_spur=20log(m/2)=-36dBc
PLL 中 reference spur 的计算
PLL 中的 reference spur 来源主要包括:
- Vctrl 节点的漏电 Ileak
- 电荷泵电流 Icp的失配
- PFD 的 timing mismatch
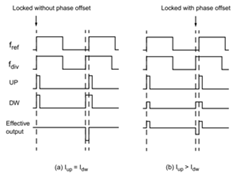
在分析这些非理想性导致的 spur 之前,我们先来考虑当理想的 PLL 中存在相差 φε 时,VCO 输出信号的 spur 的大小
由 PFD 的特性,在存在相差之后,CP 的输出电流为脉宽 Tp 为 (φε /2Pi)*Tref , 脉冲高度为 Icp, 且周期为 Tref
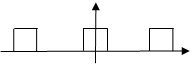
我们可以考虑之前的分析,将其傅里叶展开为正弦(或余弦)信号,求基频幅度。为方便求其傅里叶级数,可以将电流波形以下图绘出:
显见,此电流信号只有余弦分量,且其基频或一次频率的系数(或幅度)为:
可以容易看出 vco 输出信号的 spur 为:
其中 Zlpf 为 LPF 在参考频率的阻抗,考虑到 LPF 的零极点位置,我们也可将上式近似的写为:
其中 R 为 LPF 中电阻的大小, fp1 为 LPF 的极点(若为3阶的 LPF 结构,同样类似上面的方法,加上第二个极点的修正即可)
这里,进一步考虑 PLL 系统为过阻尼系统( over-damped ),可以将其看成单一极点(且极点在原点)的系统,易知其环路带宽为:
将其代入上式,有:
此处可以看出:一般性的,通过增大输入参考频率,减小带宽或者应用高阶的 LPF 都可以减小 spur , 考虑减小分频比亦可改善 spur
现在我们可以通过上面的推导来具体分析漏电和 Icp 失配导致的 Spur
Vctrl 节点的漏电 Ileak 问题
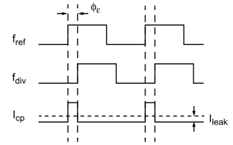
如下图所示,此时可以考虑 PLL 需要一个对应的 CP 的电流脉冲来抵消此漏电流
可以通过使周期内电荷相等来计算 CP 电流脉冲对应的相差 φε , 即
将 φε 带入之前 Pspur 的公式即可得到关于漏电导致的 Spur 的大小
注意这里可以看出,提高 Icp 的大小,可以改善漏电引起的 spur
电荷泵电流失配导致的 spur
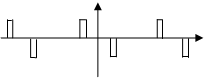
同样我们也可以找出等效的相差 φε ( Ton 为 UP/DN 同时导通时间 )
将 φε 带入之前 Pspur 的公式即可得到关于 CP 电流失配导致的 Spur 的大小
此处亦可看到,减小 UP/DN 同时导通时间,以及增大 Icp 都可以减小 spur
PFD 的 timing mismatch 导致的 vco 输出的 spur
从上图中我们可以看到,此时电荷泵电流输出由正负两个脉冲组成,净的电荷泵出为零,我们不能再使用之前的方法直接得到等效的相位误差 φε
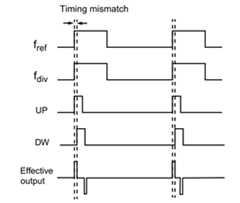
此时,可以考虑按照之前的方法,求出此电流信号的傅里叶级数
我们可以将电流波形以下图方式绘出以方便计算,同时考虑脉冲幅度为 Icp, 脉冲宽度即是 PFD 的时序失配时间 Δtd, 单周期内正脉冲的上跳沿和负脉冲的下跳沿的间隔时间为 Ton (也即是之前提到的 UP/DN 同时导通时间)
上图,可知信号只有正弦分量,且其基频或一次频率的系数(或幅度)为:
通过计算,并考虑 Ton 和 Δtd 都比较小时,上面可以化简为:
同之前分析,可以看出 vco 输出信号的 spur 为:
代入过阻尼下的环路带宽,也可得到:
显然,除了带宽和分频比的影响外,同样减小 Ton 也有助于减小 spur
上面就是关于 PLL 中 reference spure 的分析,这里的结果与李宇根的博士论文中的差别主要是计算 PFD 的 timing mismatch 导致的 vco 输出的 spur 的算式,论文中的算式中多了一个 1/sqrt(2), 具体原因尚不明.
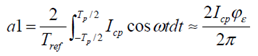
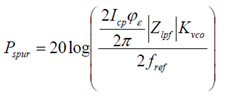
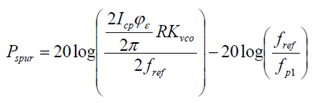
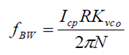
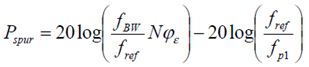
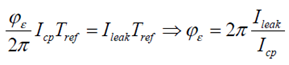
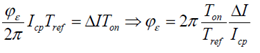
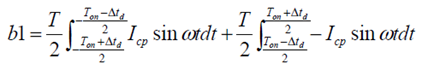
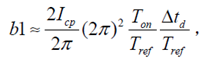
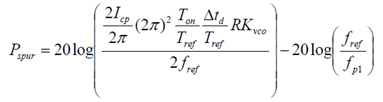
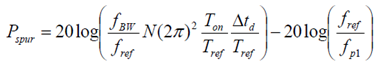
好文!
请问windknows这些都是自己一个人学的吗?我觉得好难理解啊。怎么办?
楼主,我想问一个很简单的问题,在cadence中怎么仿真参考杂散,有的说用输出频谱,有的用功率谱,并且我把输出转换成频谱感觉和论文中的结果不太一样,恳请楼主指导一下
对输出做fft
最近在搞PLL,时不时搜索到楼主的页面,解释很详细。多谢!
Pingback引用通告: 关于 spur 转换到 jitter 的计算 | Return To Innocence
相位噪声与杂散对jitter都有贡献 :as15:
就算PFD和CP是理想的,reference frequency也会被馈通到输出端吧 :as16:
这个馈通也需要一个路径的,如果用完全理想的模型,得到的vco的控制电压可以很干净