一般对电流镜的电路,谈得比较多的是其输出阻抗,以得到一个比较理想的电流源的输出;当然对于电流镜的输入阻抗,一般也要求其有较小的值,这主要是为了减小因输入电流源的有限阻抗所引起的电流的分流。此外,在考虑具体的电路中(如与电流镜相关的非主极点),小的阻抗也是我们所希望的。
High-swing cascode 电流镜的输入阻抗
对于简单的基本电流镜电路,其输入是一个二级管连接的 mos 管,很容易知道其阻抗为 1/gm; 但是对于 high-swing cascode 电流镜(如下图),就不太容易直接的看出其输入阻抗。
这里可以考虑从反馈的角度来分析:如果输入节点的电压升高,实际上也就是 Q3 的 Vgs 升高,故Ids3 变大,此电流会将输入节点的电压拉低。这实际上是一个电压负反馈(或者说是 shunt feedback),其等效阻抗应该也是一个较小的值,具体来说:
在没有反馈时,其输入阻抗 Rin 近似是:(1+gm4*ro3)*ro4;而环路增益 AL 为:gm3*(1+gm4*ro3)*ro4;故考虑反馈之后的输入阻抗为: Rin/(1+AL) , 近似为 1/gm3.
我们可以用小信号分析来验证上面的结果, 对 Q3 和 Q4 的小信号分析,可以得到:
gm3*Vin + Vd3/ro3 = Iin
gm4*(-Vd3) + (Vin-Vd3)/ro4 = Iin
求解得到:
R=Vin/Iin = (ro3 + ro4 + gm4*ro3*ro4) / (1 + gm3*ro3 + gm3*ro3*gm4*ro4)
近似为 1/gm3,可见之前反馈分析方法无误。
这里可以同样利用小信号分析的方法得到在 Q3 的漏极节点看到等效阻抗:
R=ro3/[1+gm3*ro3*(1+gm4*ro4)]
注意与一般的基本 cascode 电流镜不同,由于 high-swing cascode 电流镜中负反馈的作用,这一节点的阻抗是较 1/gm 量级更小的值。
Wilson 电流镜的输入阻抗
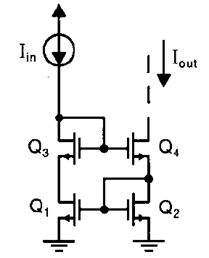
同样的,我们可也以来看下面的 Wilson 电流镜的输入阻抗
Wilson 电流镜中同样用了反馈的方式减小输入阻抗(同时也利用反馈提升输出阻抗).
未加反馈时其输入阻抗近似为: ro1 + 1/gm3,
反馈的环路增益: gm1*(ro1 + 1/gm3)*(gm4/(1 + gm4/gm2))*(1/gm2).
类似之前可以得到考虑反馈后其输入阻抗为:
R=(1/gm1)*( (gm4+gm2) / gm4),
可见其输入阻抗仍是较低的。
利用小信号分析验证可以得到类似的结果,同样也可以得到 Q1 的漏极节点的等效阻抗,不同于之前的 high swing cascode 电流镜,wilson 电流镜中的此节点的等效阻抗也为 1/gm 量级,并略小于电流镜的输入阻抗。
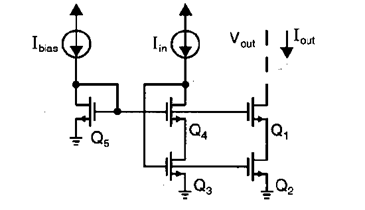
上图图一High-swing cascode 电流镜在 Q3 的漏极节点看到等效阻抗准确值为:
R=ro3*(1-gm3*ro4)/[1+gm3*ro3*(1+gm4*ro4)]
上图图一High-swing cascode 电流镜在 Q3 的漏极节点看到等效阻抗精确计算值为:
R=ro3(1-gm3*ro4)/[1+gm3*ro3*(1+gm4*ro4)]
能不能对比一下wilson和cascode电流镜的区别?感觉这两个在输入,输出阻抗和输出端最小电压方面都是一样的
应该还是有差别的,可以自己推一下
能解释下wilson电流镜的环路增益和开环增益是怎么计算的吗?
从Q1的栅极把环路断开