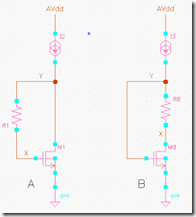
对于基本的二极管连接的 mosfet,我们都知道其阻抗约为 1/gm。在实际电路中,也有其他类似的接法,如对于下图中 A,B 分别所示的电阻方式的连接:图中 A 在考虑调零电阻对输出阻抗影响时有类似的问题,而 B 则见于自偏置方式的 cascode 接法。这里,我们来看下各自的等效阻抗的变化。
对于 A 结构
在考虑直流情况下, 电阻上没有电流流过, 实际X点和Y点电位相等, 可以认为和基本的二级管连接的电路相同, 其等效阻抗为 1/gm.
我们也可以分析其小信号电路, 注意这里考虑 X 点对地的电容 Cx, 通过分析可以得到在 Y 点看到的阻抗为: Ry=(1+s*Cx*R)*rds/[1+gm*rds+s*Cx*(rds+R)]
若忽略 rds, 可简化为:
Ry=(1/gm)*(1+s*Cx*R)/(1+s*Cx/gm),
在直流下, Ry=rds/(1+gm*rds), 同样可以看出其阻抗近似为 1/gm
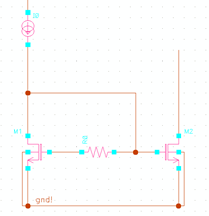
需要注意的是,若使得 R=1/gm,则 Ry 表达式中零极点可以对消,从而得到更好的频率响应,这也是有些高速电流镜采用类似结构的原因,如下图所示。
对于 B 结构
若不考虑寄生电容的影响,对电路分析可以得到:
1. Vx=Vy-Iy*R
2. Iy=gm*Vy+Vx/rds
计算简化之后, 可以得到 Y 节点的等效阻抗为:
Ry=(rds+R)/(1+gm*rds), 近似为 (1+ R/rds)/gm, 可以看出仍是 1/gm 量级。
上面的结果同样可以通过反馈的考虑得到, 只是需要注意此时的环路增益为 gm*rds 而不是 gm*(R+rds), 这实际上可以和 Cascode 的增益 gm1*ro1*(1+gm2*ro2)对比,若 Cascode 管 gm2=0,即变为简单电阻 ro2 串联在输入管上,增益变为 gm1*ro1.
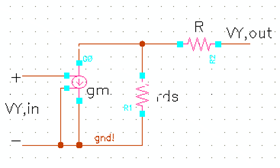
上图中将 Y 节点的反馈断开,考虑电阻 R 一端接电流源,故认为开路,因此反馈的电压
Vy,out=Vy,in * gm*rds
考虑到电路在输出为电压(并联)反馈,因此加入反馈后阻抗变为: Ry=(rds+R)/(1+gm*rds)
利用类似的分析,同样可以得到 X 节点的等效阻抗,注意此时是在 X 节点注入一个小信号电流看其等效阻抗,得到的结果与 A 结构类似:Rx=rds/(1+gm*rds)。这里需要注意的是 X 节点的等效阻抗比 Y 节点的等效阻抗更小。
你好,请问一下,对于B结构的闭环环路增益为什么是 gm*rds 而不是 gm*(R+rds),我通过二端口网络和断环的方法算出来都是 gm*(R+rds)
输出开路,R上没有电流
对于B,可以在Y点施加一个Vt,会有Vt*gm的电流流过,可以得到阻抗为1/gm
不错,另外要 rds >> R, rds 才不会对 vt*gm 电流分流
嗯,还发现可以把Y点接地,从MOS管源端往上看,这样就可以用共栅管的公式了,rin=(R+rds)/(1+gm*rds)