下面接着把关于开关变换器在非连续导通模式下的等效电路的分析过程做一些小结,这里主要还是以buck结构为例。
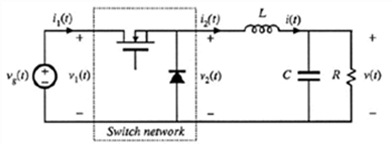
与连续导通模式的分析类似,具体方法仍然是对buck变换器中的开关网络推导其等效平均模型,即考虑在DCM工作方式时的三个状态下对应的端口变量的变化。
在具体的分析之前,对于此基本的DCM工作的buck变换器,考虑电感电流在D1T时段由零增加到其峰值ipeak,同时也在D2T时段内电感电流由此峰值减小到零,因此可以得到:
对于DCM工作下此开关网络的分析:
- 对于V1,在整个周期内都等于输入电压,因此 <v1>=vg
- 对于i1,在D1T时间内电流由零增加到其峰值, 在D2T和D3T都为零,故此可以得到其一周期内的均值为:<i1>=0.5*D1*ipeak
- 对于V2,在D1T时间内为Vg,在D2T时间内为零,在D3T时间内为V,故此其在一周期内的均值<v2>=vg*D1+v*D3
- 对于i2,在D1T时间内电流由零增加到其峰值,在D2T时间内电流峰值减小到零,在D3T时段内电流保持为零,故此 <i2>=0.5*(D1+ D2)*ipeak
将之前的ipeak , D1与D2等的关系代入上面的端口变量的计算中,并将D1换回D,得到:
在这里引入等效电阻:
则可以看到 <i1>=(<v1>-<v2>)/Re , 即输入电流可以用跨接在端口1-2之间的电阻来表征
同样,上式可以得到 <i1><v1>=<i2><v2>,适当变换之后,可以得到:
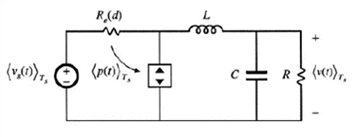
<i2> = <i1> + <i1> * (<v1> – <v2>)/<v2>, 也即可以利用输入电流和等效电阻Re的功率源之和的方式来表示输出电流,这样在加上后面的LC之后可以得到下面的等效电路:
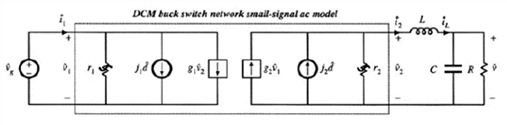
上面的得到的就是在DCM工作时的buck变换器的等效电路,为进一步得到小信号的电路,可以用与连续导通模式类似的方法,也即引入小信号扰动,获取一阶项的方式,这里可以考虑端口变量直接对引入的扰动项vg,v,d做泰勒展开的方式,最后可以得到下面方式的等效电路
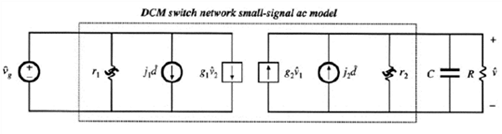
与CCM模式不同的是,在推导得到的控制到输出的表示中,实际上电容相关的极点位于低频,而电感相关的极点被移到了高频,故此上面的小信号等效可以适当地化简为如下图所示