今天的dc-dc笔记主要来对buck变换器的等效电路的推导过程做些记录,这里主要用的是平均开关模型(averaged switch model)的方法
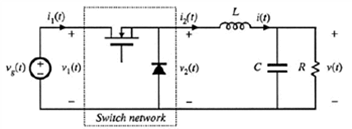
下图是一个基本的buck变换器,我们将开关和续流二极管看成一个2端口网络,对应的端口电压和电流如图中所示。
为了构建这个开关网络的等效模型,我们需要找到2个端口的电压电流均值之间的关系。首先找到其中在周期内取值相对恒定的对象作为参变量,显然<V1>=Vg不变,考虑稳态时的电感电流,也可以看出<I2>也是定值。以其为参变量,可以写出:
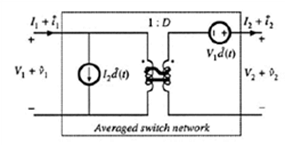
<V2>=d*<V1> 和 <I1>=d*<I2>
对其引入扰动,可以得到:
对上式化简并忽略高阶项(非线性项),可以得到:
上面的方程可以看成在直流/交流变压器的结构上再加上受控电压/电流源的结构,如下图中所示:
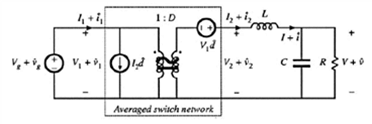
故此,完整的buck变换器等效电路:
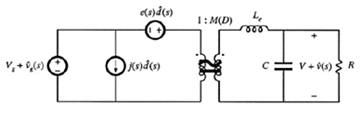
将次级的受控电压源移到左边,同时将对应的V1以及受控电流源I2写成输出电压的形式,可以得到标准的开关变换器模型
其中M(D)=D, j(s)=V/R, e(s)=V/D2
Pingback引用通告: DC-DC 学习笔记-6: buck结构的小信号传输函数 | Return To Innocence