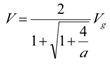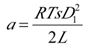继续之前的笔记:非连续导通模式(DCM)通常在发生在轻载且开关为电流单向类型时,这里对DCM工作模式下的buck变换器的做些小结
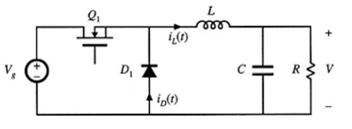
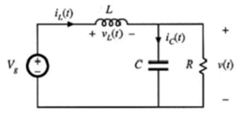
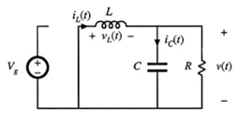
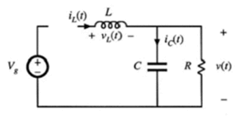
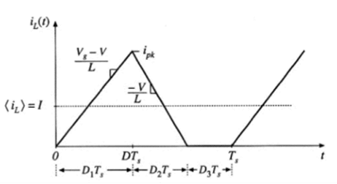
上图为基本的buck变换器的电路,考虑电路工作于DCM状态,在一个周期内,开关Q1导通的时间为D1*Ts, Q1断开并由D1提供电感电流的时间为D2*Ts,Q1断开并且D1由于不能反向导电,即电感电流为零的时间为D3*Ts,也分别对应下面的3个电路。
1. 在D1*Ts时段内,电感电压 VL(t)=Vg-V(t), 电容上的电流 iC(t)=iL(t)-V(t)/R
2. 在D2*Ts时段内,电感电压 VL(t)=-V(t), 电容上的电流 iC(t)=iL(t)-V(t)/R
3. 在D3*Ts时段内,考虑电感电流在此段时间一直为零,故电感电压 VL(t)=0,并与之前类似有:电容上的电流 iC(t)=iL(t)-V(t)/R
这里仍然考虑电感的伏秒平衡和电容的安秒平衡(或电荷平衡),考虑输出电压的ripple仍然很小,可以认为相应的电压恒定,因此伏秒平衡写为:
(Vg-V)*D1*Ts+(-V)*D2*Ts=0
对于电感电流,显然小纹波假设不再成立,但是由之前的电容电流和电感电流、负载电流的关系,以及电荷平衡仍能看出,电感电流的周期内均值应该等于负载电流,这样电容上才没有净的电荷积累。
具体的电感电流的均值可以通过下图的电感电流的波形求出,可以看到:
<iL>=0.5*(D1+D2)*D1*(Vg-V)/L=V/R
对之前的伏秒平衡和电荷平衡的两个方程化简,最后可以得到输出电压和输入电压的关系: