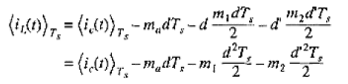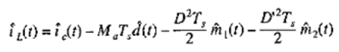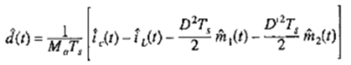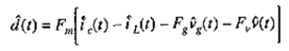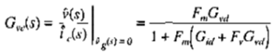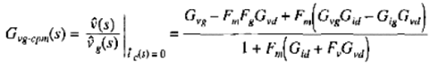之前介绍了电流模式控制的开关变换器的一阶简化模型，在简化分析中，我们假设电感电流的均值等于控制电流，在实际中电感电流的ripple并不总是能忽略的，因此需要更为完善的等效模型，这里我们对此做一些小结。

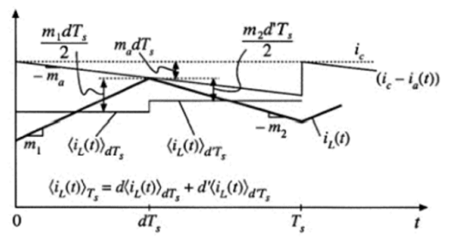
首先，对于实际电感电流的均值（与控制电流的关系），我们可以通过下图加以考虑。

上图所示为斜坡补偿后的电感电流的波形，可以看到实际电感电流的峰值与控制电流的差别为ma*d*Ts . 考虑电感电流的峰值与其平均值相差为其纹波大小，在一般瞬态情况下（包括周期开始结束时电流不等）d时段的ripple为0.5*m1*d*Ts,，d’ 时段的ripple为0.5*m2*d’*Ts, 则电感电流的均值可以写为：

对上面的电流方程引入小信号扰动（除Ts和ma不变外），可以得到：

去掉直流和高阶项，可以得到下面的小信号扰动：

考虑稳态时 D*M1=D’*M2, 上式可化简为：

并最终得到电流控制模式下的占空比的扰动的表达式：

考虑到实际上m1(t)与m2(t)由输入输出电压所控制，例如对buck变换器，有：

因此，我们可以将上式一般性的写为：

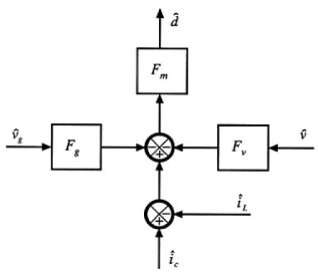
这一表示正对应下图所示。

这里的Fm=1/(MaTs), 不同变换器的Fg，Fv如下表中所示：

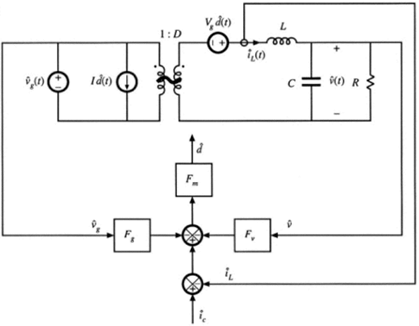
将上面的电流模式的占空比控制模型与功率级电路的等效模型结合，就可以得到电流控制模式下的变换器的等效模型，下图所示就是电流模式的buck变换器模型

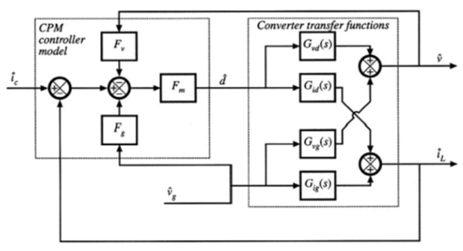
考虑主功率级电路中的电压电流的传输函数，我们可以得到下面的控制系统框图

由上面控制模型的分析，可以得到控制电流到输出电压的传输函数为：

以及输入电压到输出电压的传输函数

注意，这里我们可以回忆一下Fv和Fg的由来，实际上可以看出他们表征的是电感电流的纹波的作用，在小纹波假设下，Fv和Fg近似为零，在控制回路中只有电流反馈作用；同样对于Fm，由于斜坡电流同样会导致电感电流均值与控制电流的差别，在去除其影响后（对应Fm无穷大），上面的控制模型就变成了之前的一阶简化模型。反之，当加上很大的谐波补偿时，Fm很小，上面的传输函数近似变为一般的电压控制模式下的结果。