之前有写过关于 Reference Spur 的总结,里面有提到关于 spur 与 jitter 的转换,这里具体来谈下由 PLL 的 spur 来计算 peak-peak jitter 的问题
对于 VCO 的输出信号,考虑控制线上存在小的交流分量,此时的 VCO 输出可写为:
其中, ωo 为 VCO 的振荡频率, ωm 为 Vctrl 上的交流分量的频率,Δf 为最大频率偏移, θp ( 或 Δf/fm ) 为最大的相位偏移。
利用三角函数变换以及窄带调频的假设,上式最后可以推出:
可以看到在频谱上对应频偏 +/- ωm 处的幅度为 θp/2, 也即 Lspur=20log(θp/2)
考虑相位到时间的转换,对于 peak-peak jitter:
因此可以得到 Jpp与 Lspur的关系:
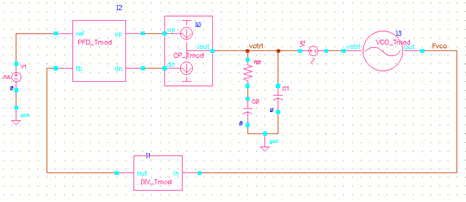
我们可以通过仿真来验证上面的结果,下图是基本的PLL的电路,其中的 PFD/CP/VCO/DIV 皆为由 verilog-A 搭建的理想时域模型,这里通过在 Vctrl 上叠加一个正弦信号源作为 spur 信号的来源。
这里的输入信号为 25MHz ( 也是 Vctrl 上的叠加的信号频率 ). DIV 为5分频,即 VCO 输出在 125MHz。
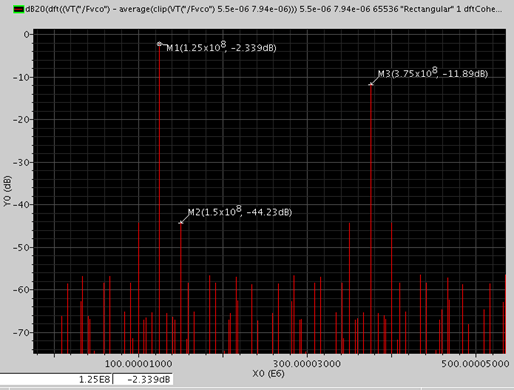
对 VCO 的输出信号做 FFT 分析,为避免频谱泄露和重复采样,选取 FFT 时间段为质数个周期 ( Reference 时钟周期 ),这里取为61个周期,在抑制直流分量后,得到如下的 fft 频谱:
可以看到 VCO 的频率处幅度为 -2.339dB, 频偏 25MHz 处幅度为 -44.23dB, 因此 Lspur=-41.891dB, 利用之前推到的 Jpp 与 Lspur 的关系,计算得到 Jpp 约为 41ps
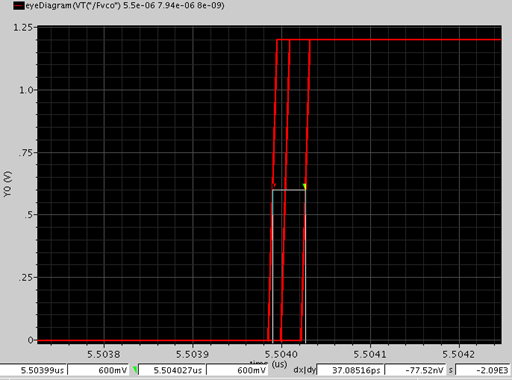
同时我们可以在时域来看实际抖动的大小,以前曾经介绍过matlab计算jitter的方法,这里为了简便,可以直接利用眼图来观测 VCO 输出的峰峰值抖动,如下图所示
这里直接测知的 Jpp 为37ps, 与之前计算得到的 41ps 还算比较接近,可见之前的峰峰值抖动与参考杂散的关系应是较为合理的。
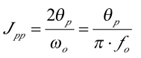
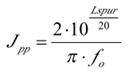
请教一下第一个Jpp的计算中,分子θp为什么要乘2,是因为Vpp=θp,然后正负半边要叠加起来吗?
我觉得你的理解是对的,Vmsin(wt)的peak-to-peak值是2Vm.
博主,请教
我在做dll jitter仿真,采用pss+pnoise仿真各个block的相噪曲线,怎么样得到怎个系统的jitter(Verilog A没有接触过)
我以前就是用 verilog-a 搭的,基本照着 designer’s guide 上方法。如果你对 matlab 之类很熟的话应该也可以直接用各个模块相噪乘以噪声传函,噪声能量在输出相加积分算jitter。