这里以基本的 RLC 电路来回顾一下关于电路中的 Q-factor (品质因数)的一些概念
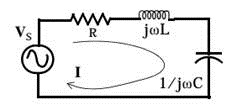
下图所示为一个简单的 RLC 串联电路
当电路工作于谐振频率时,电路中的电感的阻抗 ZL 和电容的阻抗 ZC 大小相等,符号相反,因此可以得到具体的谐振频率为:
同时,可以定义 Q 值:
同样,对于并联 RLC 电路,也有类似的定义:
一般的,品质因数可以以能量方式来加以定义,即:
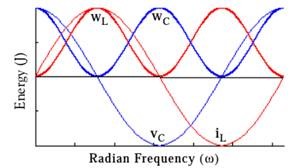
考虑之前的 RLC 电路, 在谐振频率时,电路存储的能量在电感和电容之间交换,且其最大值相等,如下图中所示。
假设电路中的电流为:
则电容上电压为:
此时电感或电容上的最大存储能量为:
电阻一周期耗散的能量为:
将其代入 Q 值的能量方式的定义中,得到的 Q 与前述定义一致,也即:
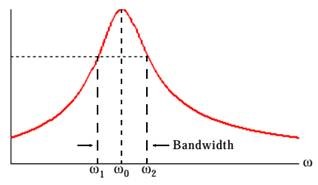
另一种关于 Q-factor 的定义主要是和带宽相关,具体可表述为:
其中,ω1 与 ω2 为 -3dB 频率, 如下图所示.
仍然考虑 RLC 串联电路,等效的导纳
其幅度特性一如上图中所示,且在 ω0 处取得最大值
考虑其分母部分,也即使电路的阻抗
对 j 乘以
同时考虑
可以得到
可见在 ω0 处, Z=R, 考虑到 ω1 处和 ω2 处导纳 -3dB 的要求,对应阻抗也即
因此要求:
对 ω 求解并取正值,可以得到
可见
也即是由带宽方式定义 Q 值的关系
此外,在 RLC 串联电路考虑输入电压到电容电压的传递函数:
也对应标准的二阶传递函数
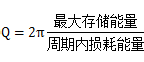
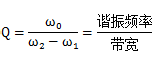
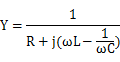
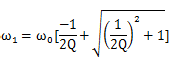
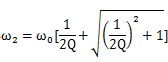
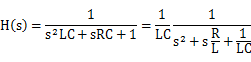
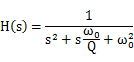
您知道为何Q等于1/2ξ吗?这个系数2是周期的意思吗?是通过泰勒展开的系数吗?