这里简单回顾一下常见的奇数分频器(3/5/7)的内容
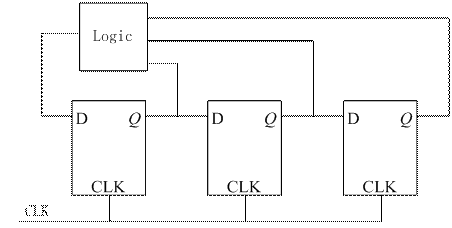
常见的分频器一般以环形计数器的形式实现, 如下图中所示, N 个 D 触发器级联, 通过对其输出处理得到信号控制环形计数器, 最大可以实现 2N 的分频
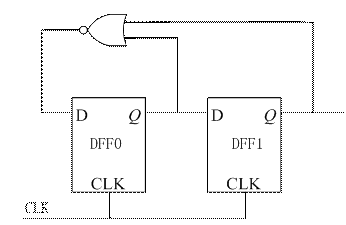
对于 3 分频电路, 需要两个 D 触发器, 考虑下面的真值表, 可以看到 D0 为 Q0 与 Q1 的或非. 这里需要注意的是, DFF 本身没有 RESET 控制, 因此需要保证电路能够由状态 ‘11’ 回到正常工作.
| Q1 Q0 | D1 D0 |
| 0 0 | 0 1 |
| 0 1 | 1 0 |
| 1 0 | 0 0 |
下图即为3分频电路的实现
5分频电路的实现, 需要3个 DFF, 首先考虑 Q2 Q1 Q0 的输出:
| Q2 Q1 Q0 | D2 D1 D0 |
| 0 0 0 | 0 0 1 |
| 0 0 1 | 0 1 X |
| 0 1 X | 1 X Y |
| 1 X Y | X Y Z |
| X Y Z | 0 0 0 |
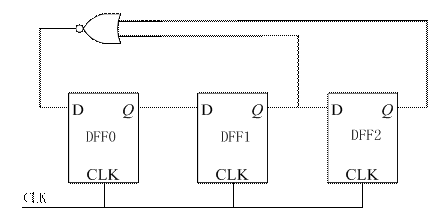
这里的 XYZ 为待定的输出(1/0), 考虑 D2=Q1,D1=Q0, 且状态不能出现重复, 因此 X=1,Y=0, Z=0, 得到实际的真值表为
| Q2 Q1 Q0 | D2 D1 D0 |
| 0 0 0 | 0 0 1 |
| 0 0 1 | 0 1 1 |
| 0 1 1 | 1 1 0 |
| 1 1 0 | 1 0 0 |
| 1 0 0 | 0 0 0 |
由此得到下面的电路实现,也可以保证其他状态亦能恢复正常.
类似5分频的过程, 我们可以得到7分频电路的真值表:
| Q2 Q1 Q0 | D2 D1 D0 |
| 0 0 0 | 0 0 1 |
| 0 0 1 | 0 1 0 |
| 0 1 0 | 1 0 1 |
| 1 0 1 | 0 1 1 |
| 0 1 1 | 1 1 0 |
| 1 1 0 | 1 0 0 |
| 1 0 0 | 0 0 0 |
从中可以看到虽然 D0 可以写为 Q2 与 Q0 的异或非, 但这样对 ’111’ 的状态会使其自锁,因此仍需由 Q2,Q1,Q0 的逻辑来得到D0