最近的工作中接触了一些开关电容电源变换器(电荷泵)的内容,在翻阅一些论文之后,感觉还是Michael. Douglas. Seeman 在他的论文中介绍的分析方法比较清楚,这里把里面的charge-multiplier-vector 方法在 0.5x 电荷泵上做一些分析和简单的验证。
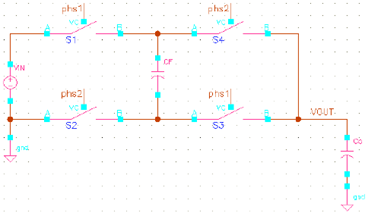
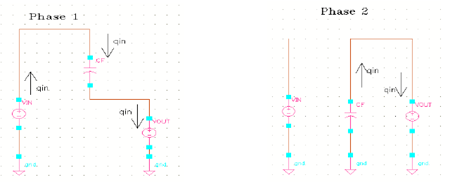
下图所示为基本的 0.5x 电荷泵,在 phase 1:开关S1, S3 闭合,S2和S4 断开, 电容Cf ( flying capacitor ) 和输出电容 Co 串联接到输入电压源; 在 phase 2:开关 S2, S4 闭合,S1 和 S3 断开, Cf 与Co并联到输出.
对上面的电路,通过简单地分析(考虑稳态时没有净电荷传输)可以得到这一电荷泵的本征增益(Vout/Vin):q=1/2. 对于理论上的最大效率,考虑系统在没有负载时的能量守恒,且能量正比于V*Q, 因此可以得到Vout/Vin=Qin/Qout=q.
考虑到 Pin=Qin*Vin*fs 以及 Pout=Qout*Vout*fs=(Qin/q)*Vout*fs. 因此电路的效率:
η=Pout/Pin=Vout/(q*Vin).
在此处,若取Vout=1.2v, q=0.5, Vin=3.3, 可以得到最大的效率约为72.7%.
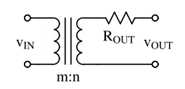
考虑到 Vout/Vin=Qin/Qout (电荷Q也可以表示等效的电流),因此我们可以考虑采用变压器的模型来表征电荷泵的特性,同时以一个等效的输出电阻来模拟负载电流的影响,如下图所示:
这里的主要问题是如何考虑 Rout,也有很多论文有不同的分析. Michael. Douglas. Seeman 在他的‘Analytical and Practical Analysis of Switched-Capacitor DC-DC Converters’ 这篇文章(以及之后的博士论文)中提出了一种基于 charge-multiplier-vector 的统一的分析方法. 下面我们就利用这种方法来对上面的电路做些分析。
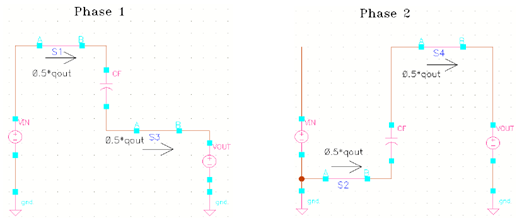
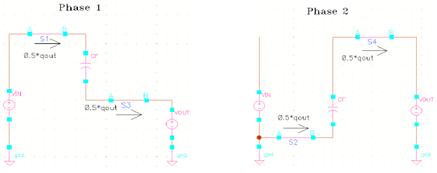
首先, 为了得到电容的电荷倍乘向量,我们将电荷泵在两个相位下的电路重新绘制于下。(注意,由于这里的输出电容Co始终接到输出,因此在这里的电路中略去) 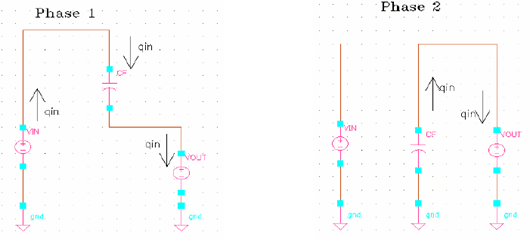
从上面的电路,我们可以得到 qout =2qin , 因此可以得到电容的电荷倍乘向量 ac :
而对于开关的电荷倍乘向量, 也可通过下面的电路加以分析。
由类似的分析, 得到开关的电荷倍乘向量 ar :
下面,我们可以计算得到在SSL (Slow Switching Limit) 和FSL (Fast Switching Limit)下的Rout.
考虑 50% 的占空比(duty cycle), RFSL 也可以写为 :
若 R1=R2=R3=R4=Ron, 则 RFSL=2Ron, 因此:
对于上面推导的结果,我们也可以做一些直观的分析:
首先, 对 SSL (slow switching limit), 电容的充放电的时间常数远小于开关周期,我们可以认为电荷在瞬间完成传输。
在 phase 1, CF 充电得到的电荷 Q=CF(Vin-2Vout), 注意这一电荷同样也流到输出(由KCL); 在 phase 2, 电容 CF 上的电荷对输出放电. 因此在一周期内流入到输出端的总电荷为 IL*Ts=2Q, 通过这两个方程,我们可以到到如前面计算的 RSSL .
其次,对于FSL (fast switching limit), 电容的充放电的时间常数远大于开关周期, 因此充放电电流可以认为恒定.同时考虑系统稳态,假设电容 CF 上的电压为Vc
在 phase 1, 电容充电电流 I1=(Vin-Vout-Vc)/(R1+R3); 在phase 2, 电容放电电流 I2=(Vc-Vout)/(R2+R4). 考虑到周期开始和结束时电容CF上没有净的电荷改变,因此D1I1=D2I2, 并且流到输出的总电荷为: IL*Ts=I1D1Ts+I2D2Ts. 联合这些方程并消去Vc, 可以得到与之前一样的RFSL 的表达式
下面我们可以通过一些仿真来对上面的结果加以验证。
对SSL, 考虑下面的电路参数:
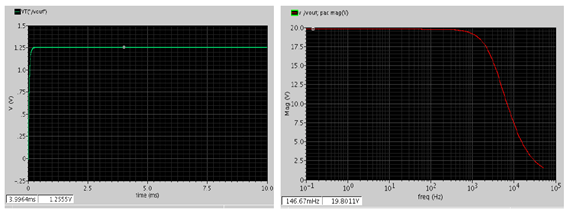
Ron=1 Ohm, CF=25 nF, Co=2 uF, fs=500 kHz (RonCF <<Ts)
对 Vin=3.3v, IL=20mA, 计算得到的 Vout 约为 1.25v, RSSL=20 Ohm. 我们可以看到与下面瞬态和PAC仿真得到的结果一致
对 FSL, 考虑下面的电路参数:
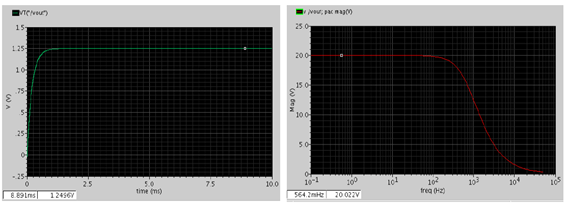
Ron=10 Ohm, CF=1 uF, Co=10 uF, fs=1 MHz (RonCF >>Ts)
对 Vin=3.3v, IL=20mA, 计算得到的 Vout 约为 1.25v, RSSL=20 Ohm. 同样我们可以看到与下面瞬态和PAC仿真得到的结果一致
最后,对于具体考虑将charge-pump工作在SSL还是FSL,可以由不同的调整(regulation)方式来决定,例如在SSL中可以采用调频的方式,而FSL中可以调整开关的等效电阻。另一个关于SSL和FSL的选择是关于面积的考虑(假设开关占据了主要的面积),我们可以具体计算SSL和FSL对于开关电阻的要求,从而决定SSL还是FSL的工作模式。
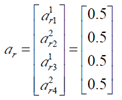
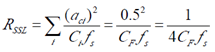
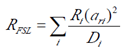
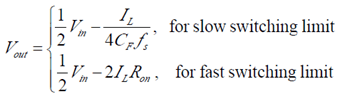
如果用duty cycle做regulation,这个方法也是值得研究的。因为digital control,或者未来的3-level都用到了。比如13年JSSC:
Fully Integrated Capacitive DC-DC Converter With All-Digital Ripple Mitigation Technique
我觉得他的理论就是有问题的,性能也很差。要不是他老板是CICC chair,想必也不会被invite。
这个确实是目前最流行的分析方法了,博主理解的也很好。
这个模型的优点是简单,易分析,精度相对高。对于片外电容,或者是parasitic小的电容情况比较适用。
缺点是没有考虑parasitic对输出电压的影响。从我measurement的结果看,我stack MIM,MOM和MOS cap一起,parasitic估计有5%,对efficiency的影响有将近4-5%。我也做了一些parasitic的分析,我觉得还是很重要的。
对于闭环charge pump的稳定性分析和建模有什么推荐的文章吗?看了一些,总感觉不是很系统。
我也没有发现特别好的
可能还是得用状态空间平均法,感觉可靠一点
关于loop 的分析,我也在做,很快应该会有文章出来。这个点目前应该还是sc converter研究的空缺。其实明年(2015)ISSCC的一篇已经有所涉及了(我师兄和我的),可以关注一下。