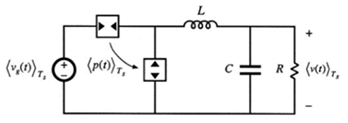
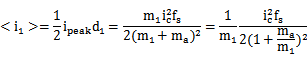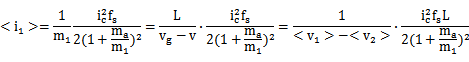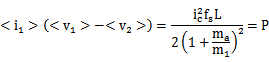之前介绍了两个电流模式控制的开关变换器的分析模型中,变换器都是处于连续导通模式,下面介绍一下变换器工作于非连续导通模式时,具体的电流控制模式的分析。
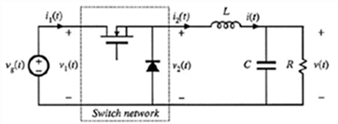
上图所示为基本的buck变换器,类似之前的分析,在DCM工作时,我们可以得到开关网络端口电压的平均值:<v1>=vg, <v2>=vg*d1+v*d3
在电流模式控制下,对于开关网络端口的电流,我们可以从下面的电感电流的波形来分析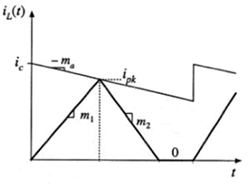
由上图,可以看到控制电流和电感电流峰值之间的关系:ipeak+mad1Ts=ic, 同时对于电感峰值电流ipeak=m1d1Ts. 因此,可以得到d1的表达式为:
端口1的电流在d1Ts时段与电感电流相同,其他时段为零,因此
端口2的电流与电感电流相同,其他时段为零,因此
考虑到m1d1=m2d2, 故此
考虑m1和m2,对于这里的buck结构, m1=(vg-v)/L, m2=v/L, 将其代入到之前的分析,除了<v1>=vg不用简化外,其他端口变量可以简化为:
对上面的个端口变量,我们可以看到
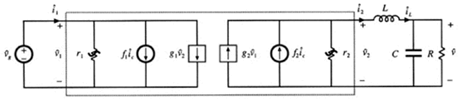
这正对应下图中的功率源的表示方法,也就是电流控制模式的buck变换器在非连续导通工作时的等效电路
对于小信号的电路,可以用之前类似的小信号扰动获取一阶项的方式,最后可以得到下面方式的等效电路