这里对 SC 积分器做一些分析,下图中所示为基本的 stray-insensitive 的开关电容积分器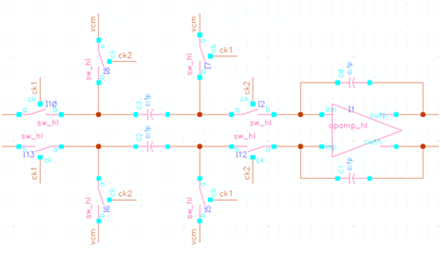
通过电荷守恒的分析,可以得到输入和输出的关系为:
这里 Cs 为采样电容,Ci 为积分电容.
对于上面的z域传输函数,可以看到极点处于原点处,也即是系统表现为积分特性。我们亦可以与连续时间的积分器比较,由 z=exp(-sT), 以及复指数的正弦表示,可以得到
考虑时钟频率>>输入信号的频率,可以近似看到
可见其积分特性与一般的连续时间积分器相同。
下面考虑运放的有限增益A,同样由电荷守恒的分析,此时的传输函数为:
可以看到此时积分器泄露,极点不在原点处 (注意上面分析未考虑运放输入节点寄生电容的影响)。
下面考虑具体此极点的频率,由上式可知,z域的极点为α,由Z= exp(-sT)=exp(j2πfT), 可以得到对应的极点频率:
这里的 fs 为采样时钟频率(之前的T即采样周期)
我们可以以实例来验证上式, 假设 Cs=Ci, 且 A=1000, 时钟频率为 10MHz, 则可以得到 α=0.999, 上式计算得到的极点频率为 1.59KHz, 这与下图中我们通过 spectre 的 PAC 仿真结构一致, 可见前面的推导无误.
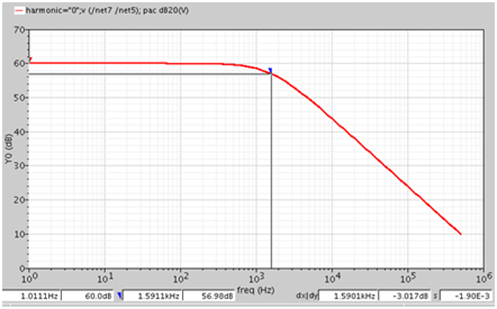
考虑有限的A时,H(z)的推导,分毫不差。
考虑有限的A时,H(z)的推导,分毫不差。