关于基本的 miller 补偿的两级运放，通常在计算输出节点的非主极点时，认为第二级的共源放大的mos管的栅和漏由补偿电容Cc短接，其阻抗近似为 1/gm, 进而得到输出的极点为 gm2/CL。但是，具体在多高的频率下可以认为 Cc 短接？也就是第二级的输出阻抗随频率具体如何变化，在何时 Cc 会使得 Rout 近似为 1/gm ? 这里，我们对此做些分析。

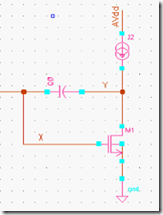
对上面的电路做小信号分析，X点考虑输入的源阻抗（或第一级的输出电阻）为Ro1，Miller电容为Cc，共源放大管的跨导gm2，输出电阻Ro2，同时忽略Y点的负载电容，通过计算，可以得到在Y点的输出阻抗为：

Rout= (1+s*Ro1*Cc)*Ro2/(1+s*Cc*((1+gm2*Ro2)*Ro1+Ro2))

可以看到，在低频下Rout=Ro2，而在零点频率ωz=1/(Ro1*Cc)之后，Rout近似为1/gm2

考虑miller补偿的二级运放，其GBW=gm1/Cc， 对一般的mosfet，有gm>1/ro, 且设计时常使输入对管的gm大于负载管的gm，故此，可以保证GBW>ωz,. 因此在计算非主极点（放在GBW外）时，认为第二级阻抗为1/gm是合适的。

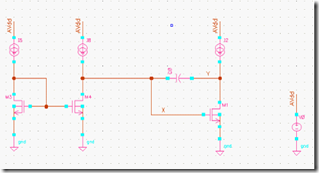
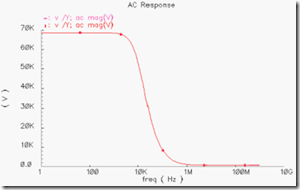
同样可以通过下面的仿真来了解下实际是否与上面的分析一致，通过在输出节点注入ac=1的交流电流，通过AC分析，得到的输出的电压就是其小信号阻抗

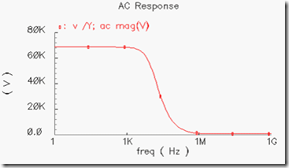
具体得到的阻抗特性如下，和之前的分析还是比较一致的。

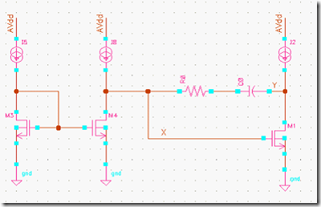
实际的 miller 补偿的运放设计中, 常采用如下图中的调零电阻 Rc 来消去右边平面零点，我们还是要考虑下这个电阻会否影响最后的 Rout。

通过同样的小信号分析, 我们一样可以得到输出节点的阻抗:

Rout=Ro2(1+s*Cc*(Rc+Ro1))/(1+s*Cc*((1+gm2*Ro2)*Ro1+Rc+Ro1))

考虑这里 Rc 略大于 1/gm2, 通过类似的简化, 可以看到最后整个阻抗特性和未加 Rc 时的阻抗特性基本类似, 我们通过比较下图中两者仿真的结果, 也可看出.