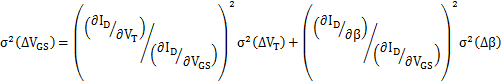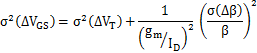在集成电路的设计中,常需要考虑电路中各元件的匹配(mismatch)问题,特别在 foundry 的 model 没有提供统计参数来做 monte-carlo 分析时,需要设计人员利用 foundry 的文档中的参数对集成电路中器件的随机失配做一些估计,因此有必要了解一些器件匹配的统计模型。这里对这一问题简单来小结一下。
关于集成电路中器件的随机失配,可以用一简单的模型来加以描述:
其中,A 为器件随机失配的参数,通常在设计手册中给出;B 为测试带来的失调,通常可认为为零; W 和 L 为器件的宽长(um单位); S 为对器件间距的敏感参数; D 为两器件的间距。
如果忽略器件间距的影响(考虑具体版图设计时的优化),上面的模型可以进一步简化为:
对这一特性的进一步应用,我们可以得到 MOSFET 的阈值电压 VT 和电流因子 β 的失配为:
通常 VT 与 β 的相关性可以认为很低,因此近似看成独立的随机变量。这样,我们可以分析它们各自导致的 MOSFET 电流 ID 和栅-源电压 VGS 的失配。
一般在常用的偏置情况下(Vdsat<500mV), 可以认为 ΔID 与 ΔVGS 都是 VT 的 mismatch 占主导。
对于集成电路中的电阻和电容也有类似的 mismatch 模型:
对于具体的失配参数,除了查看工艺文档中的描述,也有一些粗略估计,例如对于 .18工艺而言:可以近似估计 AVT=5mVμm, Aβ=1%μm;对 P-poly 电阻,AR 可以估计为 1~2%μm; 对 MIM Cap, AC 可以估计为 5%μm。