说起来，之前也有用过利用电感截断交流，电容截断直流来仿真反馈环路的环路增益的频率响应，但是对于电感电容在低频时对其的影响一直没特别考虑过。前两天看到有关于此的讨论，回去翻了下‘The Designer’s Guide to Spice and Spectre’上的介绍，确实在相关仿真方法比较的图中有示出。

下图是利用LC来仿真放大器频率响应的电路，通常会把L,C值取较大（我一般都取1G），现在为了比较直观的看到LC的影响，将其取如图大小，图中的运放用宏模型描述，增益A=500，f-3db=500KHz


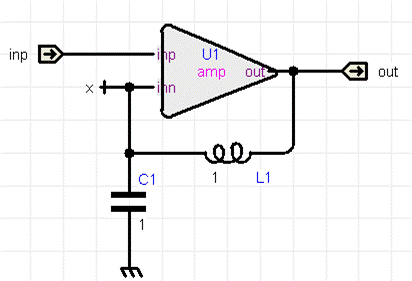
仿真得到电路的频率响应，图中红线为幅度响应（刻度在左），蓝线为相位响应（刻度在右）

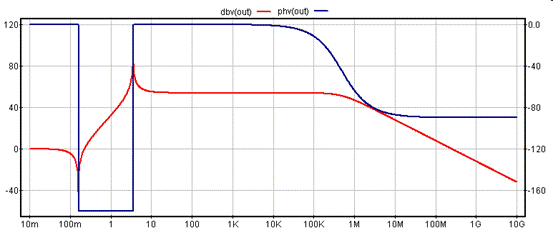
可以看到此时LC对其低频下有较大的影响

若考虑运放为理想增益级（带宽无限），可以比较容易推出LC引入的零极点
zero=+-j*sqrt(1/R*C); pole=+-j*sqrt((A+1)/R*C)
零点在极点之前，由于零点为虚轴上的共轭零点，会在幅度响应中有负的peaking，同样极点产生正的peaking，与图示中较为相像。

如考虑运放为之前的单极点系统，同样求解，得到的零点不变，但极点发生变化，此时的极点方程为
(1+L*C*s^2)(1+s/p)+A=0， p为2*Pi*f3db 为运放原来的极点
利用matlab的符号运算（symbolic math）求解（solve命令），得到的值仍比较复杂，但可看到运放极点已发生改变。利用subs命令代入L,C,A,p的大小，求极点，显示结果LC对其极点影响基本可以忽略（此例中，至少小数点四位后）

将L,C都取回到1G大小，看其频响曲线，LC影响基本可忽略，亦可由之前推导零极点看出

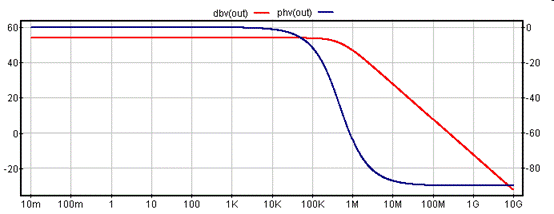
这种方法的另一个问题是 L 截断环路时, 实际可能改变负载, 从而引入误差. 但具体如何评估其影响, 现在还没有看到比较好的方法.

‘ The Designer’s Guide to Spice and Spectre ’ 似乎推崇的是 Middlebrook 的方法, 感觉有点麻烦, 主要还是用在环路互相 loading 不好直接断开的时候, 另外不知道 cadence 里面的 stb 仿真用的是什么方法…